
This week we are going to bump the dimensions of our systems and talk about how simple rules can produce unexpectedly complex, structured and hard to predict behaviour. We'll have a quick overview on the academic history as well as some useful nomeclatures to compare and challenge classic approaches to Cellular Automata.
On elementary cellular automata the state is represented on a unidimensional space (1D). A bidimensional image (2D) can be created by stacking the state over time.
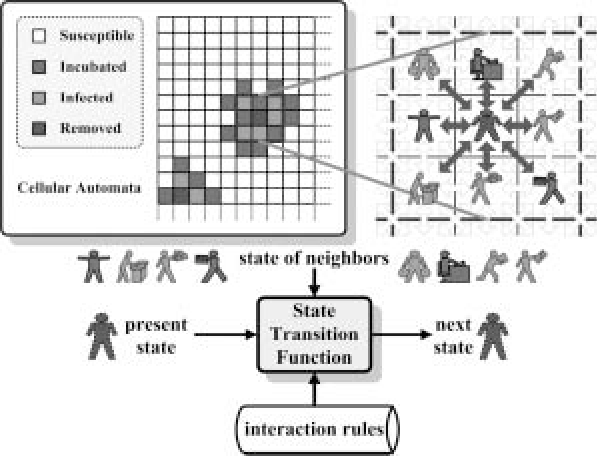
A common way to picture cellular automata is to visualise the state on a 2D squared grid.
Cellular automata can operate on multi dimensional state space, shapes and neighborhoods. A brief history of Cellular Automata.
Although, in theory, computation can be achieved on elementary cellular automata, most of its practical examples occur on 2D space.
A lot of possible cellular automata will generate either empty, repetitive or chaotic patterns. A lot of attention has been given at the edge of chaos.
Cellular automata are a great way to visualize how complex behavior can emerge from simple parts and rules.
An animation can be made by displaying the 2D grid spaces as frames. A sculpture can be made by stacking the 2D grid spaces as layers. What else?
What’s up with the fixation about universal computation?